最長共同部分子序列(Longest Common Subsequence,LCS)是動態規劃入門第一個經典應用。這個問題最早起源於對 DNA 序列的比對問題:如果有兩段很長很長的 DNA 序列,那麼他們到底有多接近呢?比方說有些文獻講猩猩跟人類的 DNA 有 98% 像、有 96% 像、有 88-92% 像、或是有 87% 像。要怎麼定義這個相似程度是一個可以討論的問題。在電腦科學方面,我們喜歡把東西抽象化——比方說直接把 DNA 序列定義成一個字串之類的。於是我們可以試圖定義什麼叫做「兩段 DNA 的相似程度」。
我們說一個字串 X 是 A 的子序列(Subsequence),當 X 可以是藉由 A 剔除某些字元、並且把剩下的字元按照順序拼起來變成的字串。而最常共同部分子序列的問題,就是要找出某個 X,使得 X 同時是 A 和 B 的子序列。我們先來看看實作吧~
https://leetcode.com/problems/longest-common-subsequence/
給定兩個字串 text1 以及 text2。請你找出他們最長共同部份子序列的長度。
一時沒頭緒?沒關係!如同大多數的演算法題目一樣,只要觀察邊界的地方,通常都可以找到遞迴的切入點!我們來考慮兩個字串的最後一個字元。以 python 流派的寫法就是 text1[-1] 與 text2[-1] 這兩個字元。如果這兩個字元相同,那麼一種可能的答案就是兩邊同時去掉最後一個字元時的最長共同部份子序列、加上這個字元。如果最佳解不同時包含兩字串的最後一個字元,那麼它總來自於去掉 text1 的最後一個字元、或去掉 text2 的最後一個字元以後,兩個字串的最長共同部份子序列的長度。
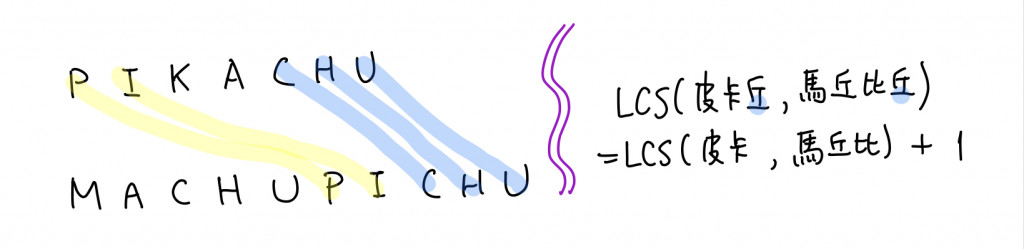
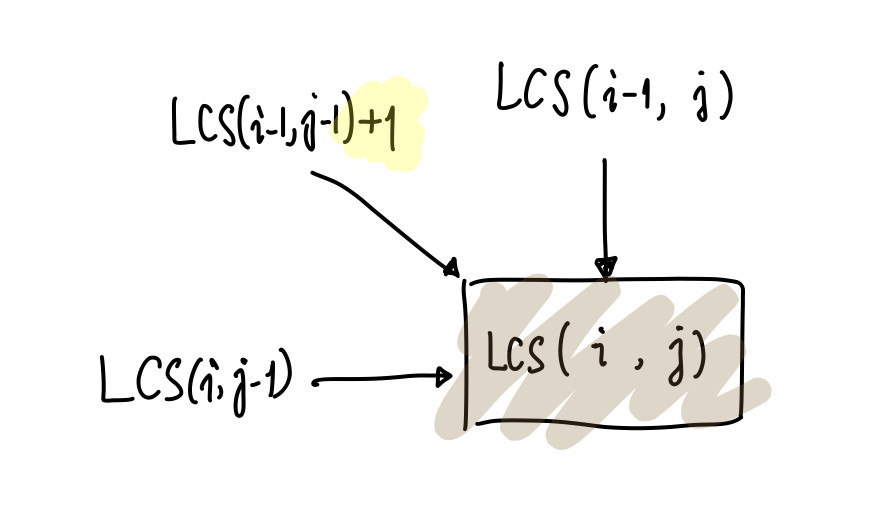
此時我們對於子問題的刻劃也就能字元其縮了!令 LCS(s1, s2) 表示兩個字串的 LCS 長度,那麼根據上述討論便有三種可能的 case 需要考慮:LCS(s1[:-1], s2[:-1]) + 1、LCS(s1[:-1], s2)、LCS(s1, s2[:-1])。注意到我們所需要的所有參數,都是原本 text1 與 text2 的前綴啊!所以可以用 (i, j) 來表示 s1 的前 i+1 個字元與 s2 的前 j+1 個字元。這麼一來就可以回到填表的方法,從小的 (i, j) 開始處理囉。
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
m, n = len(text1), len(text2)
dp = [[0] * n for _ in range(m)]
for i in range(m):
for j in range(n):
if text1[i] == text2[j]:
dp[i][j] = 1 if (i == 0 or j == 0) else (dp[i-1][j-1] + 1)
if i > 0 and dp[i-1][j] > dp[i][j]:
dp[i][j] = dp[i-1][j]
if j > 0 and dp[i][j-1] > dp[i][j]:
dp[i][j] = dp[i][j-1]
return dp[m-1][n-1]
對於長度超級長的 DNA 序列來說,其實 的演算法是非常沒有效率的。不過好消息是,如果 LCS 的長度相當大,那麼小幅度修改上面的動態規劃程式碼,就可以獲得一個
時間複雜度的動態規劃!稍微掐指一算,可以發現在
常數 的時候,這個方法是線性的,很優。從這個方法出發,再次利用神秘字串匹配演算法(比方說後綴樹)加速的話,還可以得到一個
的演算法,這樣可以讓
的時候達到最優解唷,簡直是解優雜貨店呢。讀者們如果有興趣可以想想看~
有沒有更快的解呢?目前 LCS 遇到的超大障礙:強指數時間假說。因此大家普遍不相信 LCS 在最壞情形下能做得比 快。如果只是想要找到近似解的話,2018 年剛好有一篇論文做到常數倍數的近似解,如果答案是 LCS 的話,他可以找到 LCS/3400 以上長度的答案 :D,而時間複雜度可以做到
,打破了平方屏障!
